지난 번 야구 게시판에 투구수와 투구 이닝에 대하여라는 제목으로 졸고(拙稿)를 올렸던 적이 있습니다. (블로그 포스트 링크는 여기) 평균 투구수보다 더 적은 투구수로 이닝을 마치는 투수들은 기대치보다 더 많은 이닝을 투구할 수 있으며, 이것이 이닝 이팅의 한 요인으로 작용할 수 있다. 이 정도가 제가 글을 통해 말씀드리고 싶었던 점이리라고 봅니다. 그리고 글 말미에 삼진을 많이 잡고 볼넷을 많이 내주는 투수들이 그렇지 않은 투수들보다 투구수가 많다, 는 말씀을 덧붙였습니다.
이에 대해 young026 님께서 좋은 지적을 해주셨습니다. 삼진은 투구수에 영향을 끼치지 않는다는 말씀이었습니다. 그 말씀을 듣고 생각해 보니, 삼진은 아웃 카운트와 곧바로 직결되기 때문에 아웃 카운트를 잡아 낸 다른 투구와 비교해 손해볼 게 없다는 생각이었습니다. 반드시 볼을 세 개 이상 던져야 한다는 생각에 투구수에 영향을 줄 것이라고 생각했지만, 평균 투구수라는 걸 생각해 보면 세 개는 그리 많은 숫자가 아닐 수도 있던 겁니다. 오늘은 이에 대해 데이터를 통해 한번 확인해 보고자 합니다.
데이터는 역시 young026 님께서 자료실에 올려주신 선수/팀 통산 투타 성적을 사용했습니다. 프로 원년부터 2003년까지 최소 60이닝 이상을 투구한 투수 가운데 상대 타자, 투구수, 출루율이 모두 나와 있는 선수를 추려본 결과 표본 약 950개를 구할 수 있었습니다. 확인 도구는 회귀 분석을 통해 계산한 R-square(R²)값입니다.
혹시라도, R²값에 대해 잘 모르고 계시는 분들이 계실까 봐, 간략히 설명드리도록 하겠습니다. 타율이 2할 5푼인 타자가 있습니다. 이 선수는 하루에 평균 30분을 연습했습니다. 그러다 '타율 2할 5푼이면, 점마 집에 가야 하는기다.'하는 팬의 우려 섞인 목소리를 듣고 연습 시간을 30분 더 늘렸습니다. 그랬더니 타율이 2할 6푼으로 올랐습니다. 연습을 하면 타율이 올라간다는 사실에 기뻐한 타자는 연습 시간을 30분 더 늘렸습니다. 그러자 다시 타율이 2할 7푼이 됐습니다. 다시 30분을 늘렸고, 2할 8푼이 됐습니다. 이렇게 된다면, 우리는 30분 연습 시간을 늘릴 때마다 타율이 1푼씩 올라간다는 사실을 발견할 수 있습니다. 이를 공식으로 정리하면 ;
타율 = .250 + 0.01 × 30 ÷ n
그런데 수학적으로야 이런 일이 생길 수 있겠지만, 실제로 이렇게 딱딱 맞아떨어지기는 힘들겠죠? 자, 그럼 한번 변화를 줘 보겠습니다. 저기서 30분 더 연습량을 늘렸다고 칩시다. 그랬더니 타율이 2할 9푼이 된 게 아니라 2할 8푼 5리에서 더이상 올라가지 않았다. 그럼 저 공식에 변화가 생기게 됩니다. 이를 그래프로 그려보면 ;
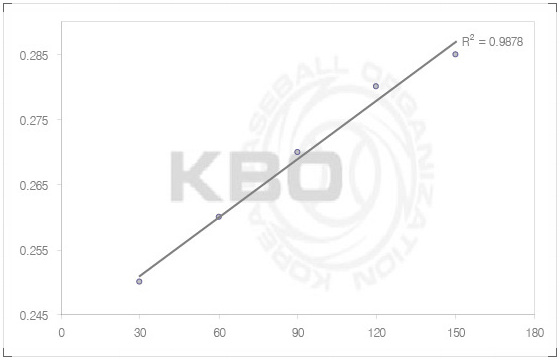
점 위치는 이해가 가실 겁니다. 그런데 가운데 선이 하나 그어져 있습니다. 그건 뭐냐, 저 점들을 그냥 연결해서 그래프를 그릴 수도 있겠습니다만, 각 점들이 위치하고 있는 지점간 최단 거리를 선으로 이은 것입니다. 전체적인 변화 정도를 측정하기 위해서 말입니다. 그리고 그 옆에 적혀 있는 R² 값은, 가장 쉽게 생각하자면, 저 그래프 기울기가 되겠습니다. 그러니까 위에 보시는 그래프 기울기가 0.9878 정도 되는 것입니다. 그리고 지금껏 우리가 함께 추리해 온 과정을 살펴 보면, 30분 더 연습할 때 타격이 1푼 증가할 확률이 98.78%라고 이해하셔도 무방하겠습니다. (아주 쉽게 쉽게 생각하자면 이렇다는 뜻일 뿐입니다 ^^;)
상식적으로 인정할 수 있는 자료를 가지고 그래프를 한번 더 그려보도록 하겠습니다. 이닝당 상대 타자가 많은 건 피출루율이 높기 때문이다. 그렇겠죠? 이를 그래프로 그려보면 ;
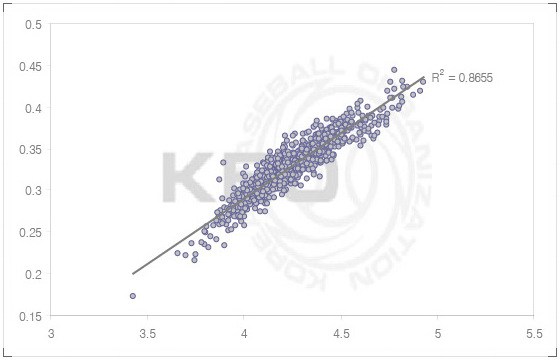
R²값이 0.8655로 나타납니다. 다시 위의 논리를 그대로 따르자면, 예를 들어 타자 1명을 더 상대할 때 출루율이 1푼 늘어날 확률은 86.55%다, 정도가 될 것입니다. 희생플라이라든가 수비 실책 같은 건 출루율에 포함되지 않으니 나머지 예외도 있을 겁니다.
자, 이제 자료가 어떻게 만들어 지는지 확인하셨습니다. 그럼 한번 하나씩 보도록 하겠습니다.
1) 상대타자당 투구수가 적으면 이닝당 투구수가 적다?
저는 사실 상대 타자, 투수당 투구수 그러니까 P/PA는 타자에게는 의미 있는 기록이라고 생각하지만 투수에게는 그렇지 않다고 생각합니다. 전혀 중요하지 않다는 게 아니라 P/IP 즉 이닝당 투구수가 더 중요하다고 생각한다는 뜻입니다. 타자당 공 3개밖에 안 던지지만 줄줄이 홈런을 맞는다면, 전혀 효율적인 투구를 했다고 볼 수 없기 때문입니다. 그래서 먼저 이 그래프를 한번 그려봤습니다.

R²=.5912, 연관성이 있기는 하지만 꼭 그렇게 될 정도 비율이라고 말하기는 어렵습니다.
2) 이닝당 투구수가 많은 건 K+BB의 숫자가 많기 때문이다?
자, 이제 초점을 P/PA보다는 P/IP에 맞추도록 하겠습니다. 2)는 제가 지난 글에서 주장(?)했던 내용입니다. 맞을까요?

R²=0.4370, 글쎄요, 생각보다 R²값이 떨어집니다.
3) 이닝당 투구수가 많은 건 BB를 많이 허용하기 때문이다?
그럼 정말 young026 님 말씀 대로 BB 때문일까요?

R²=.5015, 확실히 아까보다는 R²값이 올라갔습니다. 반대로 말씀드리면, 삼진은 투구수에 별 영향을 못 미친다는 뜻이 아닐까요?
4) 삼진이 많은 건 이닝당 투구수를 늘린다?

R²=.1282, 그렇습니다. 이 정도면 확실히 별 영향을 못 끼친다고 하겠습니다. 단순히 2), 3), 4) 놓고 보자면, P/IP에 가장 큰 영향을 끼치는 건 볼넷입니다. 그리고 위에서 확인해 보신 것처럼 더 큰 영향을 끼치는 건 출루율이겠죠. (너무 당연한가요? ^^;)
5) 삼진을 많이 잡는 투수들이 볼넷도 더 많이 내준다?
이건 사실 어떻게 보면, 거의 상식처럼 받아들이게 되는 내용입니다. 정말 그럴까요?

R²=0.003, 이 정도면 거의 랜덤입니다. 사실 개인적으로는 제가 기존에 가지고 있던 K/9와 K/BB는 중복되는 지표가 아니다, 는 생각을 다시 한번 확인해 볼 수 있는 기회가 됐다고 생각합니다.
